Números mistos — como 2 ½ ou 5 ¾ — são mais que simples exercícios escolares. Eles aparecem em receitas, na venda de madeira e até na medição de distâncias em esportes.
Números Mistos vs. Frações Impróprias
Se você já mediu 2 ½ xícaras de farinha ou ouviu alguém dizer que correu 5 ¾ milhas, já lidou com números mistos. Um número misto combina um número inteiro com uma fração própria — como 3 ½, que representa três inteiros e mais metade. São práticos, familiares e usados no dia a dia mais do que imaginamos.
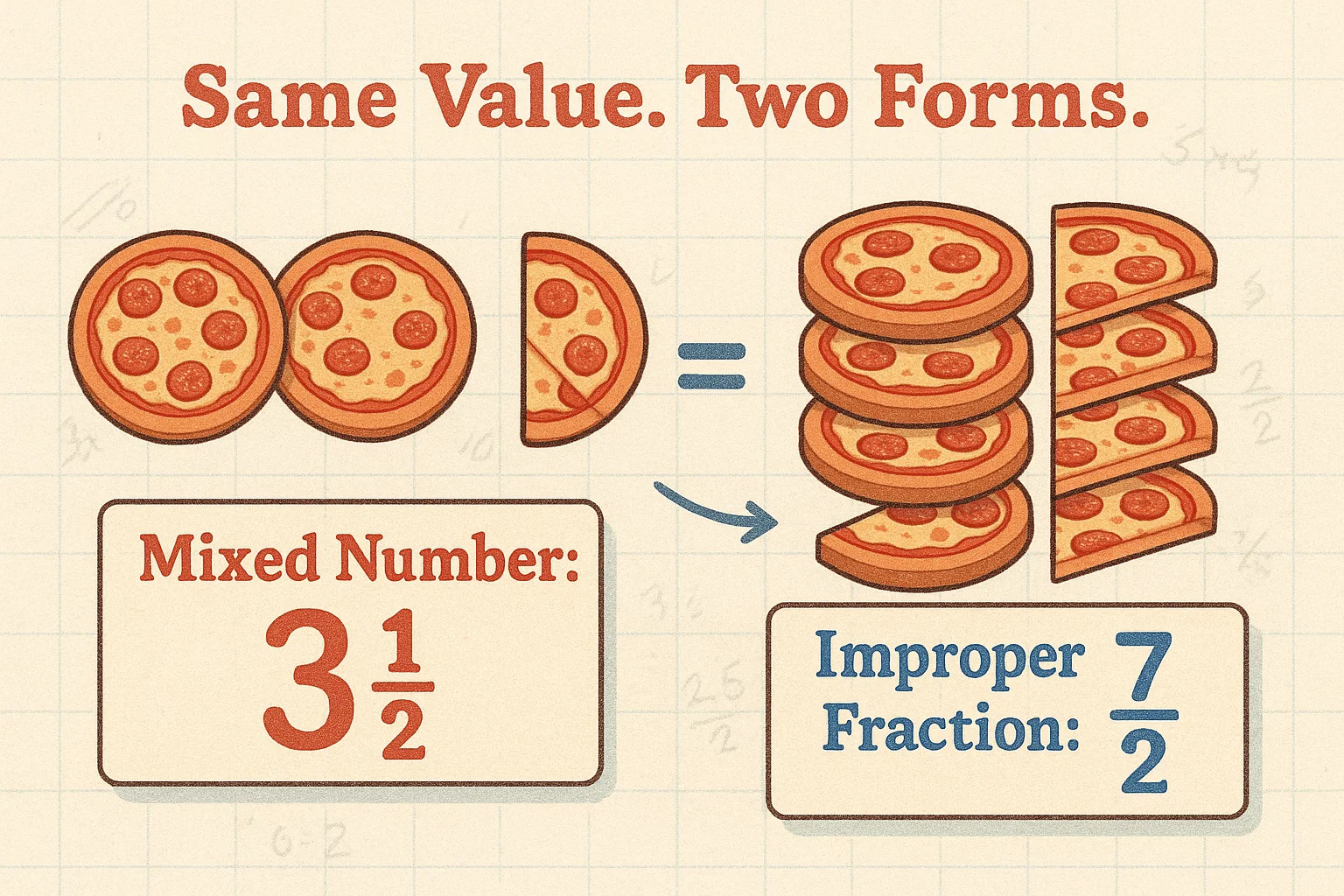
Por outro lado, frações impróprias parecem mais complexas, mas seguem a mesma lógica matemática. Nessas frações, o numerador (número de cima) é igual ou maior que o denominador (de baixo) — por exemplo, ⁷⁄₂. O valor é o mesmo que 3 ½, só que representado de forma diferente.
Então, por que usamos formas diferentes para o mesmo valor? Números mistos são mais fáceis de entender rapidamente, enquanto frações impróprias facilitam cálculos, especialmente em álgebra ou programação.
Como converter um número misto em fração imprópria:
Considere o número 4 ⅗.
Multiplique o número inteiro pelo denominador: 4 × 5 = 20
Some o numerador: 20 + 3 = 23
Coloque sobre o denominador original: ²³⁄₅
Portanto, 4 ⅗ vira ²³⁄₅.
Esse processo é comum ao converter números mistos em frações impróprias antes de multiplicar ou dividir.
Como converter fração imprópria em número misto:
Pegue a fração ¹¹⁄₄.
Divida o numerador pelo denominador: 11 ÷ 4 = 2 resto 3
O quociente é o número inteiro (2), e o resto (3) é o novo numerador
Mantenha o denominador original: 2 ¾
Assim, simplificamos para número misto partindo da fração imprópria.
Curiosidade: “Durante a missão Apollo 13, engenheiros da NASA usaram réguas de cálculo e cálculos manuais com frações como 2 ⁵⁄₈ para redirecionar rapidamente a nave e salvar a tripulação.” — arquivos da NASA¹
Como os Números Mistos com Frações são Calculados
Ao somar, subtrair, multiplicar ou dividir números mistos, há um equilíbrio entre os números inteiros e as frações. O segredo? Manter o cálculo simples, organizado — e sempre simplificar ao final. Seja para dobrar uma receita ou resolver uma prova, estas regras rápidas ajudam a ser ágil e preciso.
Somar e Subtrair
Comece separando a parte inteira da fracionária. Os números mistos têm ambas, então trabalhe cada uma separadamente e depois junte os resultados.
Vamos a um exemplo:
Somar: 2 ½ + 3 ¾
Soma dos inteiros: 2 + 3 = 5
Soma das frações: ½ + ¾ → converta para denominador comum → ²⁄₄ + ³⁄₄ = ⁵⁄₄
Agora temos: 5 + ⁵⁄₄ → como ⁵⁄₄ = 1 ¼, a resposta final é:
→ 6 ¼
Subtrair: 5 ⅚ − 2 ⅔
Inteiros: 5 - 2 = 3
Frações: ⁵⁄₆ − ²⁄₃ → converta ²⁄₃ para ⁴⁄₆ → ⁵⁄₆ − ⁴⁄₆ = ¹⁄₆
Resposta final: 3 ¹⁄₆
Se a subtração resultar em fração negativa (por exemplo, ¼ − ¾), talvez seja necessário pedir emprestado do número inteiro. Não pule esta etapa — é onde muitos erros acontecem. Também é possível verificar o resultado simplificado com o Cálculo de Fração Simplificada.
Multiplicar
A multiplicação de números mistos sempre começa pela conversão.
Suponha que queira multiplicar: 2 ⅓ × 1 ½
Converta ambos para frações impróprias:
2 ⅓ = ⁷⁄₃
1 ½ = ³⁄₂Multiplique:
⁷⁄₃ × ³⁄₂ = ²¹⁄₆Simplifique:
²¹⁄₆ = 3 ½
Agora sim, estamos avançando.
Fato Interessante: “Um estudo em uma escola de Chicago mostrou que alunos que praticaram a conversão de números mistos antes de multiplicar melhoraram suas notas em 27% comparados aos que calcularam pela intuição visual.” — Estudo do Departamento de Educação dos EUA²
Multiplicação é mais direta porque usa números completos, sem a necessidade de um denominador comum como na soma ou subtração. Se não tiver certeza do resultado, faça o cálculo no papel e depois use uma Calculadora de Frações para conferir.
Divisão
A divisão costuma assustar, mas nada mais é que multiplicação disfarçada.
Vamos tentar: 3 ¾ ÷ 1 ½
Converta para frações impróprias:
3 ¾ = ¹⁵⁄₄
1 ½ = ³⁄₂Inverta a segunda fração (divisor):
³⁄₂ vira ²⁄₃Multiplique:
¹⁵⁄₄ × ²⁄₃ = ³⁰⁄₁₂Simplifique:
³⁰⁄₁₂ = 2 ½
Pronto — inverta e multiplique.
Se o resultado ficar numa forma imprópria como ²¹⁄₄, pode manter assim para álgebra ou textos formais, ou converter para número misto (5 ¼) para o uso cotidiano.
Seja na sala de aula ou na cozinha, entender esse processo dá confiança para lidar com qualquer cálculo — por mais confuso que pareça. Também pode verificar seus passos com o Cálculo Matemático.
Quando uma Fração Salvou uma Obra
Números mistos importam não só em sala, mas podem economizar tempo, dinheiro e salvar projetos inteiros.
Um encarregado de obra em Des Moines, Iowa, contou como uma medida mal interpretada quase comprometeu a reforma de uma escola. A planta previa 8 ⅜ polegadas para acabamento de metal personalizado. Um aprendiz, sem experiência em frações, leu 8.3 polegadas. O resultado? Painéis de alumínio curtos demais — quase ¹⁄₁₆ polegada, suficiente para reprovar na inspeção.
O erro custou uma semana inteira de retrabalho e mais de $4.000 em materiais.
“Aprendi do jeito difícil — números decimais nem sempre ajudam. Números mistos é o que a fita métrica real usa. É ⅜, não 0.375, e essa diferença pode custar seu salário.” — Tim Vega, líder de construção, Vega & Sons Build Co.⁴
Hoje, antes de enviar medidas para fabricação, a equipe confere uma tabela impressa de frações para decimais fixada em todas as caixas de ferramentas — e novos contratados recebem aula rápida de adição e subtração com denominadores comuns.
Números mistos não são só teoria. Aparecem em plantas, receitas, notas fiscais, estatísticas esportivas e calibração de ferramentas. Dominar seu uso é estar preparado para o dia a dia, fita métrica na mão.

- NASA. “Cronologia Apollo 13.”
- Departamento de Educação dos EUA. “Estudo de Matemática no Ensino Médio.”
- Programa de Panificação e Culinária do Napa Valley College, entrevistas informais, março 2023
- Entrevista com Tim Vega, junho 2022. Normas de Construção e Inspeção, Departamento de Segurança Pública de Iowa

