Cálculo de Desvio Padrão

O desvio padrão é um daqueles termos que você provavelmente ouviu na escola — talvez em uma aula de matemática ou em algum relatório de pesquisa. Mas por trás do nome intimidador há um conceito surpreendentemente intuitivo que sustenta tudo, desde descobertas científicas até estratégias de negócios e previsões meteorológicas. Em termos simples, é a forma como entendemos a dispersão — o quão afastados os valores estão do centro, sejam eles notas de teste, preços ou resultados de pacientes. Saber medir a variabilidade nos dá clareza, contexto e confiança nos dados que usamos todos os dias.

Confira Matemática para acessar mais ferramentas

O que exatamente é o desvio padrão?

O desvio padrão mede o quão espalhados estão os valores em um conjunto de dados. Pense nele como a resposta para a pergunta: “Quanto os números se afastam da média?”

Suponha que um professor aplique um teste e toda a turma tire exatamente 80 em 100. A média é 80, e todos os alunos atingiram esse valor — então o desvio padrão é zero. Não há nenhuma variabilidade. Agora imagine uma segunda turma com a mesma média de 80, mas com notas de 60, 70, 90 e 100. Embora a média ainda seja 80, as notas estão bem distribuídas. Essa segunda turma terá um desvio padrão muito maior.

Um desvio padrão baixo significa que os pontos de dados estão concentrados em torno da média; um desvio padrão alto indica que estão mais dispersos.

Por que nos importamos com a variabilidade dos dados?

A variabilidade não é apenas ruído estatístico — ela conta uma história. Ao medir o quanto os dados flutuam, o desvio padrão nos ajuda a identificar tendências, valores atípicos e padrões ocultos. Na saúde, é usado para avaliar se um tratamento tem efeitos consistentes. Na climatologia, auxilia no acompanhamento de variações incomuns de temperatura ao longo do tempo. Educadores o utilizam para analisar o desempenho dos alunos em diferentes escolas, enquanto engenheiros dependem dele para controle de qualidade. Sem compreender a variabilidade, corremos o risco de interpretar mal o que os dados realmente indicam.

Experimente também ferramentas relacionadas: ferramenta de cálculo da média, ferramenta de cálculo da variância ou ferramenta de cálculo do escore Z para explorar outras formas de analisar seus dados.

Desvio Padrão Populacional

Quando você dispõe dos dados de toda a população que está estudando, pode calcular o desvio padrão populacional sem precisar estimá-lo. Esse método permite determinar com precisão o grau de variabilidade de todo o conjunto de dados, como quando se tem informações de todos os indivíduos de uma população ou de todos os pontos de uma pesquisa abrangente.

Fórmula do desvio padrão populacional:

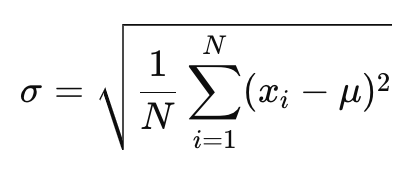
Onde:

𝜎: desvio padrão populacional,

𝑁: número de observações no conjunto de dados (tamanho da população),

x_i: cada valor do conjunto de dados,

𝜇: média da população.

Desvio Padrão Amostral

Esse cálculo é usado quando você tem apenas uma amostra de dados que representa a população. Como não é possível dispor dos dados completos da população, o desvio padrão amostral ajuda a estimar o desvio padrão populacional com base na amostra disponível. O desvio padrão amostral inclui uma “correção” para compensar o viés potencial na estimativa, garantindo que não subestimemos o grau de dispersão.

Fórmula do desvio padrão amostral: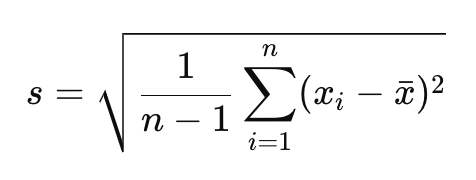

Onde:

𝑠: desvio padrão amostral,

𝑛: número de observações na amostra,

x̄: média da amostra.

Curvas de Sino e Distribuições Normais

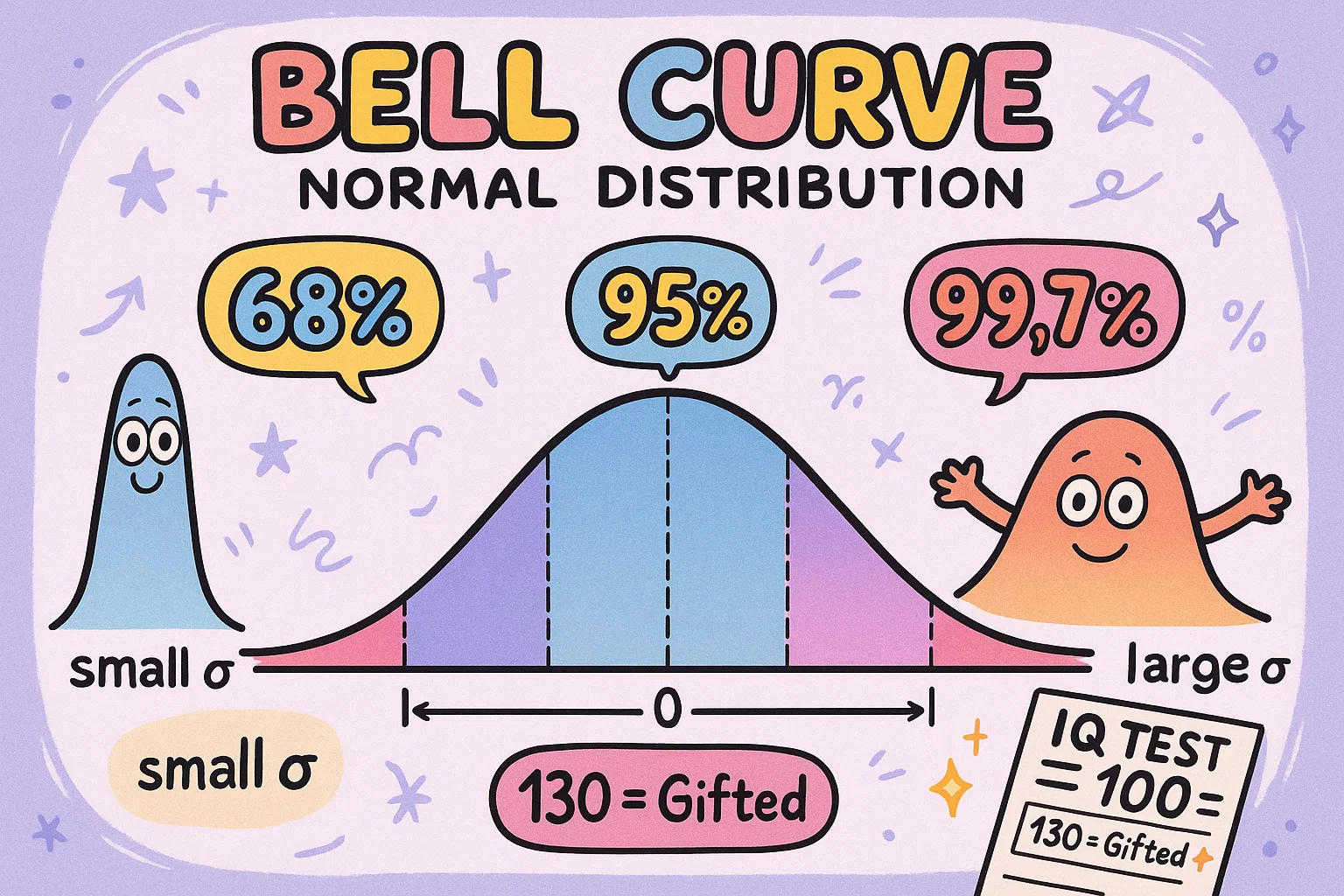
Você provavelmente já viu uma curva de sino — aquele gráfico suave em forma de morro, onde a maioria dos valores se concentra no meio e poucos aparecem nos extremos. Não é apenas um desenho elegante. Ele representa a chamada distribuição normal e surge frequentemente na vida real: alturas, testes de QI, resultados de exames e até medições de pressão arterial.

É aí que o desvio padrão entra em cena. Ele controla a largura dessa curva. Se a maioria dos números estiver próxima da média, a curva será estreita e alta — indicando um desvio padrão pequeno. Mas se os valores estiverem mais dispersos, a curva se alarga e fica mais baixa, o que significa um desvio padrão maior.

Há uma regra prática:

• 68% dos valores estão dentro de 1 desvio padrão da média

• 95% dentro de 2 desvios padrão

• E 99,7% dentro de 3 desvios padrão

Isso facilita muito entender o quão comum (ou incomum) um valor é — seja em notas de teste ou em retornos de ações.

🎯 Curiosidade: A maioria dos testes de QI é construída para seguir a curva de sino — com média de 100 e desvio padrão de 15. É por isso que uma pontuação de 130 é considerada de alto rendimento!