Cálculo da Área do Retângulo

O retângulo é uma das formas mais reconhecidas na matemática e no cotidiano. Desde projetos de jardins até planos arquitetônicos e problemas de geometria em sala de aula, saber calcular a área de um retângulo com precisão e agilidade é uma habilidade essencial. Neste guia, exploraremos como usar um cálculo da área do retângulo, aprofundando o significado da fórmula, exemplos práticos, curiosidades interessantes e até acidentes históricos. Ao final, você ganhará não só confiança prática, mas também uma compreensão mais ampla do alcance da geometria no mundo real.

Quer aprender sobre outras formas? Experimente nossa coleção completa de calculadoras de área.

O que é o Retângulo

Quando pensa em retângulo, provavelmente surgem objetos comuns como livros, janelas e telas de smartphones. Retângulos estão por toda parte, tão comuns que muitas vezes não percebemos sua verdadeira complexidade.

Na geometria, o retângulo é classificado como um quadrilátero, ou polígono de quatro lados, em que cada ângulo é exatamente 90 graus. O que distingue os retângulos é que seus lados opostos são iguais em comprimento e perfeitamente paralelos. Imagine esticar um quadrado em uma direção — essa figura alongada é um retângulo.

Civilizações vêm usando retângulos há milhares de anos. Construtores antigos escolhiam pedras retangulares para erguer paredes e templos, confiando no equilíbrio e estabilidade da forma. Engenheiros e arquitetos atuais continuam preferindo os retângulos por sua simetria, que simplifica cálculos e favorece designs robustos.

Uma forma fácil de imaginar um retângulo é pensar em um piso de azulejos — cada azulejo representa uma parte do todo. Visualizar uma superfície preenchida por unidades quadradas idênticas ajuda a entender o conceito principal da medição de área.

Apesar da simplicidade, os retângulos exercem papéis importantes em diversas áreas, da arquitetura e design de telas à arte, engenharia e física. Compreender o funcionamento dos retângulos abre portas para reconhecer padrões geométricos em ambientes digitais e físicos

Quer comparar retângulos a outras formas? Experimente o Cálculo da Área do Quadrado para figuras com lados iguais, ou o Cálculo da Área do Paralelogramo para quadriláteros inclinados.

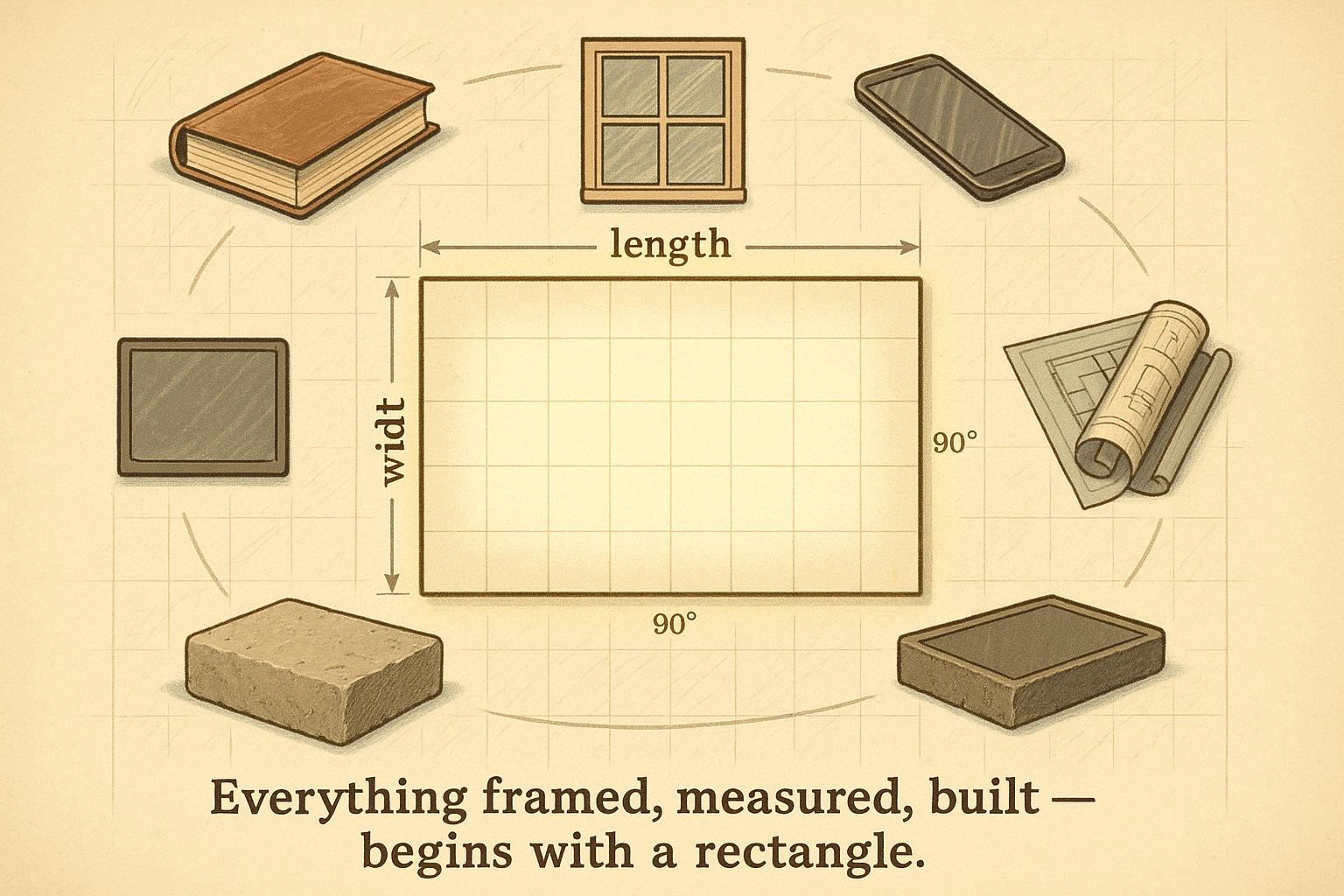
Como Calcular a Área do Retângulo?

Uma das primeiras habilidades em geometria que a maioria aprende é como calcular a área do retângulo — e é uma competência que permanece, porque é muito útil. Seja para estimar o revestimento do piso ou medir uma parede para papel de parede, esse cálculo básico economiza tempo e esforço.

A fórmula básica é:

Área = comprimento x largura

Onde:

• Comprimento: o lado mais longo do retângulo

• Largura: o lado mais curto do retângulo

• Resultado: expresso em unidades quadradas (m², ft², in², etc.)

Passos específicos:

Passo 1: Meça o Comprimento e a Largura

Use uma régua ou fita métrica para medir os dois lados do retângulo. Anote as medidas cuidadosamente.

Exemplo: Uma escrivaninha tem 5 pés de comprimento e 3 pés de largura.

Passo 2: Verifique se as Medidas Usam a Mesma Unidade

Antes de calcular, confirme que comprimento e largura estão na mesma unidade.

• 1 metro = 100 centímetros

• 1 pé = 12 polegadas

Precisa de ajuda para converter unidades? Experimente nosso cálculo de área para garantir medidas consistentes antes de multiplicar.

Passo 3: Aplique a Fórmula

Multiplique o comprimento pela largura.

Passo 4: Apresente a Área em Unidades Quadradas

Dependendo das unidades de entrada, o resultado estará em m², ft², in², etc.

Dica Rápida: Confira sempre suas unidades — um detalhe pequeno que faz grande diferença para obter a área correta.

Depois de entender esse processo, você vai se surpreender com a frequência com que esse conhecimento é útil — seja para estimar espaço no chão, projetar embalagens ou resolver questões acadêmicas.

O Grande Desastre no Palco

Em 1959, uma equipe de produção da Broadway projetou uma plataforma retangular para o palco que deveria se encaixar perfeitamente na área dos bastidores — com 30 pés de comprimento por 20 pés de largura. Mas alguém na equipe confundiu a medida da largura e usou polegadas em vez de pés.

O resultado? A plataforma acabou quase dois pés mais larga do que deveria.

Durante o ensaio final, tentaram colocar a plataforma no lugar — mas ela emperrou na entrada, bloqueando artistas e cenários. O resultado foi um caos nos bastidores poucas horas antes da estreia.

Num esforço desesperado, a equipe teve que serrar o excesso, repintar e reorganizar parte do espetáculo durante a noite.

Nota: Sempre confira as dimensões do seu retângulo — e suas unidades.