Ferramenta básica de cálculo de frações

As frações aparecem em tudo — receitas, construção, impostos, até na hora de dividir uma pizza. Dominar o cálculo de frações economiza tempo, evita erros e dá confiança a estudantes e profissionais. De somar ⅔ + ¼ a multiplicar ⅝ × ¾, este guia explica cada passo, esclarece dúvidas comuns e mostra como as frações se aplicam a situações do dia a dia.

O que é uma fração?

Uma fração representa uma parte de um todo. É escrita com dois números empilhados e separados por uma linha — o número de cima é o numerador (a parte que você tem) e o de baixo é o denominador (o total de partes que compõem o todo).

Imagine uma pizza: se ela for cortada em 8 fatias iguais e você comer 3, você consumiu 3⁄8 da pizza. O 3 indica suas fatias, e o 8 representa a pizza inteira.

As frações estão presentes o tempo todo, não só na aula de matemática. Em receitas, costuma-se usar ½ xícara de açúcar ou ¾ de colher de chá de sal. Na construção e na medição, elas são indispensáveis — como numa tábua com 5⁄8 de polegada de espessura. Também surgem ao dividir uma conta entre amigos ou calcular um desconto.

Exemplos do dia a dia:

• Meia torta: ½

• Três quartos de tanque de combustível: ¾

• Cinco oitavos de polegada na régua: 5⁄8

As frações deixam os números mais flexíveis — elas ajudam a descrever medidas que não cabem em números inteiros.

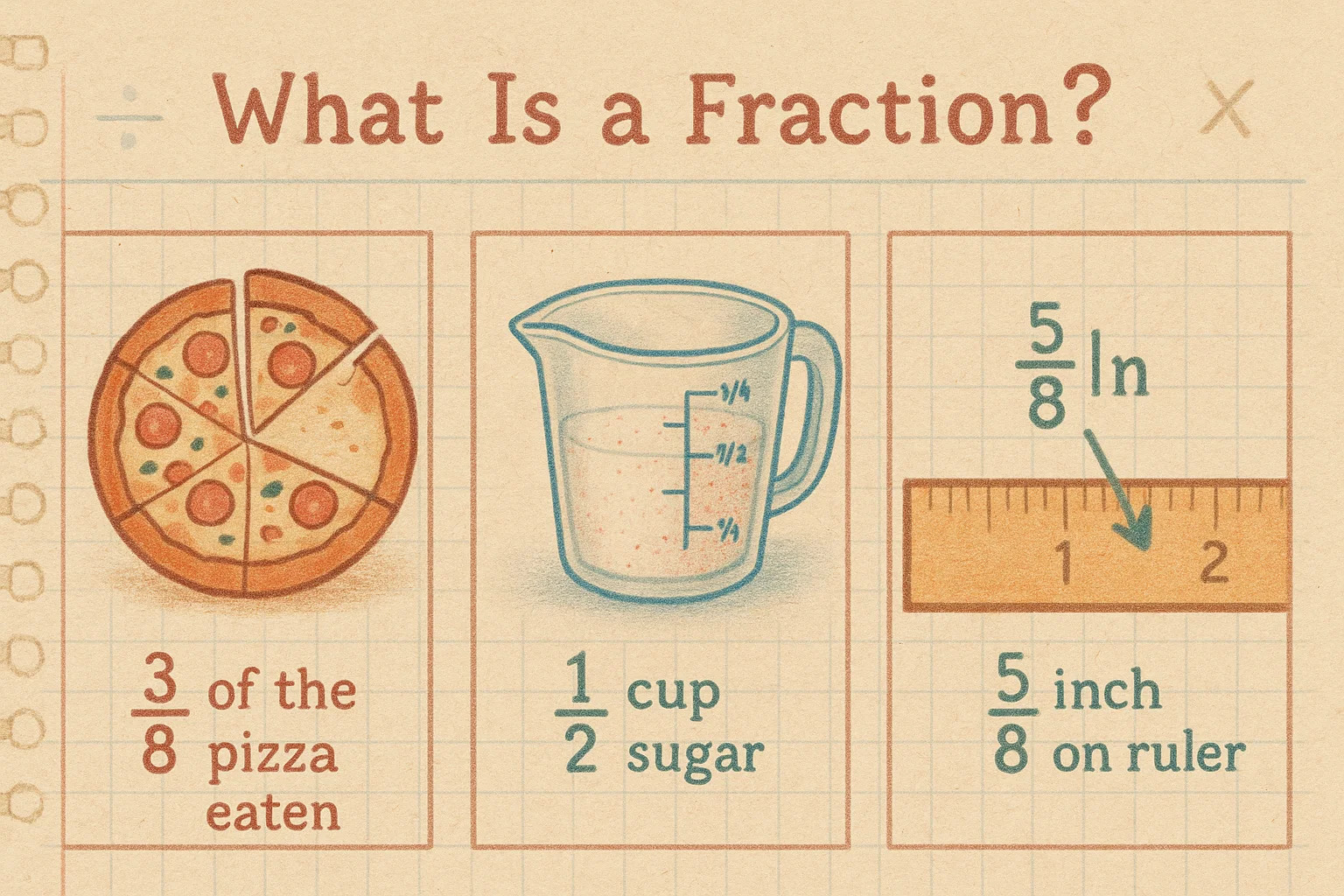
Somando frações

Somar frações é simples quando elas já têm o mesmo denominador — basta adicionar os numeradores e manter o denominador.

Por exemplo: 1⁄4 + 2⁄4 = 3⁄4

Mas, se os denominadores forem diferentes, é preciso igualá-los antes. A forma mais fácil é encontrar um denominador comum — normalmente o mínimo múltiplo comum (MMC) dos dois denominadores. Depois, ajuste as frações para que compartilhem esse denominador e some-as.

Exemplo com denominadores distintos: 1⁄3 + 1⁄6

• O denominador comum é 6.

• Reescreva 1⁄3 como 2⁄6.

• Agora some: 2⁄6 + 1⁄6 = 3⁄6.

• Simplifique dividindo numerador e denominador por 3: 3⁄6 = ½.

Atalho rápido: se um denominador for múltiplo do outro (como 2 e 4), não é preciso achar o MMC completo: use diretamente o maior denominador.

Subtraindo frações

Subtrair frações segue quase os mesmos passos de somar — só que com sinal de menos.

Se elas têm o mesmo denominador, basta subtrair os numeradores e manter o denominador:

5⁄8 − 3⁄8 = 2⁄8, que simplifica para 1⁄4.

Quando os denominadores são diferentes, encontre primeiro o denominador comum (normalmente o MMC). Depois, reescreva cada fração com esse denominador e subtraia:

Exemplo com denominadores distintos:
5⁄6 − 1⁄3

• O denominador comum é 6.

• Reescreva 1⁄3 como 2⁄6.

• Agora subtraia: 5⁄6 − 2⁄6 = 3⁄6.

• Simplifique: 3⁄6 = ½.

Se, após ajustar, o numerador da fração menor for maior, o resultado fica negativo. Exemplo:
1⁄4 − 3⁄4 = −2⁄4 = −½.

Obs. rápida: Você pode converter respostas negativas em números mistos, mas deixar como fração imprópria (−5⁄4) costuma ser aceitável na maioria dos exercícios.

Multiplicando frações

Multiplicar frações costuma ser a operação mais simples — não há necessidade de igualar denominadores. A regra é direta: multiplique os numeradores entre si, multiplique os denominadores entre si e, por fim, simplifique se possível.

Veja o passo a passo:

Exemplo: 2⁄3 × 3⁄5

1. Multiplique os numeradores: 2 × 3 = 6.

2. Multiplique os denominadores: 3 × 5 = 15.

3. Combine: 6⁄15.

4. Simplifique dividindo por 3: 6⁄15 = 2⁄5.

Funciona da mesma forma para frações próprias (1⁄2) ou impróprias (7⁄4).

Outro exemplo com números maiores: 5⁄8 × 4⁄10

1. Numeradores: 5 × 4 = 20.

2. Denominadores: 8 × 10 = 80.

3. Fração resultante: 20⁄80.

4. Simplifique: divida por 20 e obtenha 1⁄4.

Um atalho útil é o cancelamento cruzado antes de multiplicar. Se um numerador e um denominador têm um fator em comum, reduza-os primeiro para manter os números menores: 6⁄10 × 5⁄9

• Antes de multiplicar, veja que 10 e 5 têm fator comum.

• Simplifique 5⁄10 para 1⁄2.

• Agora o problema é 6⁄2 × 1⁄9 = 3 × 1⁄9 = 3⁄9 = 1⁄3.

Curiosidade:
Multiplicar por uma fração menor que 1 sempre reduz o resultado. Por exemplo, ¾ × ½ = ⅜, que é menor que ambas as frações iniciais.

Dividindo frações

Dividir frações pode parecer complicado no começo, mas é apenas um passo a mais que multiplicar. Em vez de dividir diretamente, você inverte a segunda fração (recíproco) e depois multiplica como de costume.

A regra “inverter e multiplicar” funciona sempre porque dividir por uma fração é o mesmo que multiplicar pelo seu inverso.

Exemplo: ¾ ÷ ½

1. Mantenha a primeira fração: ¾.

2. Inverta a segunda (½ vira ²⁄₁).

3. Multiplique: ¾ × ²⁄₁ = ⁶⁄₄.

4. Simplifique dividindo por 2 para obter ³⁄₂.

5. Opcional: converta em número misto: 1½.

Outro exemplo: ⁵⁄₆ ÷ ¹⁰⁄₉

1. Inverta ¹⁰⁄₉ para ⁹⁄₁₀.

2. Multiplique: ⁵⁄₆ × ⁹⁄₁₀ = ⁴⁵⁄₆₀.

3. Simplifique dividindo por 15, resultando em ¾.

Dica rápida: dividir por uma fração menor que 1 tende a aumentar o resultado, enquanto dividir por uma fração maior que 1 tende a diminuir.

Aplicação prática: se uma receita pede ¾ de xícara e você quer só metade da quantidade, na verdade faz ¾ ÷ 2. Usando a regra, é ¾ × ½ = 3⁄8 de xícara.

Fato para lembrar: nunca divida frações igualando denominadores. Inverta a segunda e multiplique — é mais rápido e evita erros.

Como as operações com frações se relacionam com ideias matemáticas mais amplas

Às vezes, as frações parecem só mais um assunto da escola, mas elas aparecem por toda parte quando você começa a prestar atenção — e não apenas em prova de matemática. Ao somar, subtrair, multiplicar ou dividir frações, você usa conceitos que se conectam a situações cotidianas e até a tópicos avançados sem perceber.

Pense nisso:

• Proporções e receitas: Quando você reduz ⁸⁄₁₂ para ²⁄₃, não está apenas simplificando — está definindo uma proporção. Essa mesma relação ajuda a dobrar uma receita de biscoitos ou ajustar ingredientes para meia fornada.

• Álgebra sem mistério: Resolver algo como x ÷ ¾ = 2 é o mesmo truque clássico — inverta ¾ para ⁴⁄₃ e multiplique. São frações fazendo o trabalho por trás de uma equação.

• Conversões de unidades que você usa: Já trocou Fahrenheit por Celsius? A fórmula envolve a fração ⁵⁄₉. Ou talvez tenha convertido milhas por hora em metros por segundo — tudo graças às frações.

• Probabilidade: Jogando um dado de seis faces, a chance de tirar 4 é ¹⁄₆. Calcular a probabilidade de dois eventos é somar ou multiplicar frações, mesmo sem perceber.

As frações são mais que números com linha no meio — são ferramentas para entender relações, escalas e mudanças. Quando você nota como aparecem o tempo todo, elas deixam de ser tarefa de casa e viram atalhos que você já sabe usar.

Curiosidade: os antigos egípcios escreviam quase todas as frações com 1 no numerador. Para representar ²⁄₃, por exemplo, eles somavam ½ + ¹⁄₆. Funcionava, mas nossas frações modernas são bem mais práticas.