Calculadora de Volume de Elipsóide

Vamos ser sinceros—"elipsóide" não faz parte do nosso vocabulário diário. Mas, surpreendentemente, elipsóides estão ao nosso redor. Já segurou um ovo, arremessou uma bola de rugby ou viu a Terra do espaço? Você já encontrou um. Para todos os tipos de formas 3D—de cones a pirâmides—você encontrará tudo na página principal do Calculador de Volume.

O Que É Exatamente um Elipsóide?

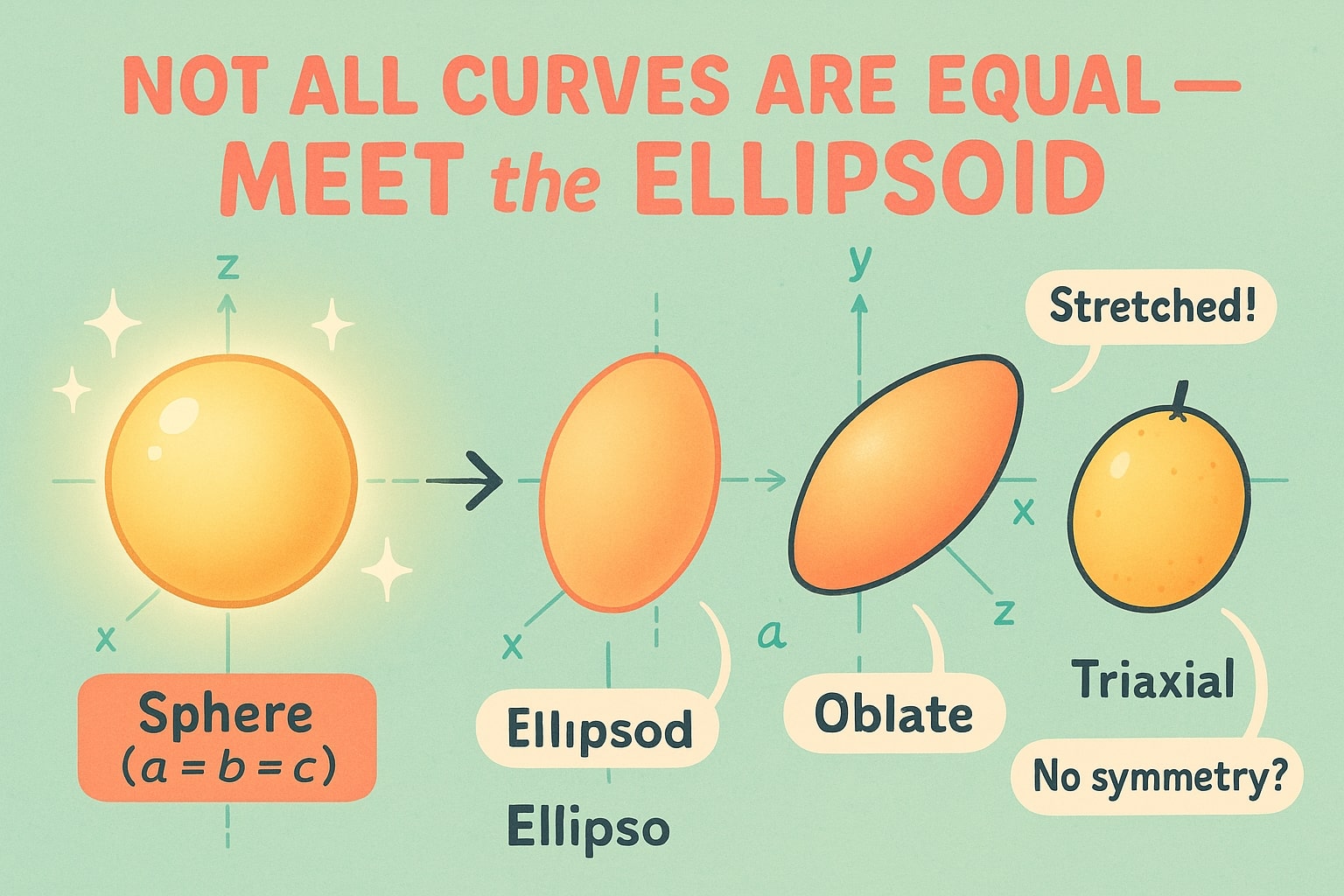
Comece com uma esfera—um objeto 3D perfeitamente redondo. Agora imagine achatá-la suavemente ou esticá-la de lado. Essa forma arredondada e suave que não é igual em todas as direções? Isso é um elipsóide.

Em termos geométricos, um elipsóide é descrito usando três eixos:

• a = comprimento ao longo do eixo x

• b = comprimento ao longo do eixo y

• c = comprimento ao longo do eixo z

Se a, b e c forem iguais, parabéns—você está olhando para uma esfera. Mas quando eles diferem, você está no território do elipsóide.

Existem alguns tipos comuns:

• Elipsóides prolados: alongados em um eixo (como uma bola de rugby)

• Elipsóides oblados: achatados em um eixo (como a Terra!)

• Elipsóides triaxiais: todos os três eixos diferentes (sem simetria—pense em frutas de formato irregular ou cápsulas de remédio)

Desde a forma de planetas até células e até ovos de peixe, elipsóides aparecem mais do que se imagina. Por isso, saber como calcular seu volume é realmente útil.

Depois de calcular o volume, você pode convertê-lo rapidamente em litros, galões ou outras unidades usando o Conversor de Volume.

Como Calcular o Volume de um Elipsóide

Aqui está a boa notícia: a fórmula do volume é surpreendentemente simples. Se você conhece os três semi-eixos (a, b e c), basta usá-los nesta fórmula:

Volume = (4/3) × π × a × b × c

É isso. Você multiplica os três semi-eixos, depois multiplica por pi (π) e em seguida por quatro terços.

Nota Rápida: Certifique-se de estar usando os semi-eixos, não os diâmetros completos. Se seu elipsóide tem 10 cm de largura, deve usar 5 cm para esse eixo na fórmula.

Suponha que seu elipsóide tenha semi-eixos de 4 cm, 3 cm e 2 cm.
Você calcularia o volume assim:

Volume = (4/3) × π × 4 × 3 × 2 = (4/3) × π × 24 ≈ 100,53 cm³

Agora, se os três semi-eixos forem iguais—digamos, 5 cm cada—seu elipsóide é na verdade uma esfera. Nesse caso, a fórmula simplifica para a clássica:

Volume = (4/3) × π × r³

💡 Dica Profissional: Se sua forma é quase esférica, você pode estimar o volume usando a fórmula da esfera—ou facilitar a vida com nossa Calculadora de Volume da Esfera.

Gauss e a Forma da Terra

No início do século XIX—muito antes dos satélites ou do Google Earth—um matemático alemão chamado Carl Friedrich Gauss fez uma pergunta ousada: qual é, realmente, a forma da Terra?

A maioria supunha que fosse uma esfera perfeita. Mas Gauss tinha dúvidas. Ele suspeitava que a Terra fosse ligeiramente achatada nos polos—o que hoje chamamos de elipsóide oblato. Em vez de apenas teorizar, ele saiu a campo: escalou montanhas, carregou equipamentos e desenvolveu novos métodos para medir longas distâncias com notável precisão.

Seus esforços pioneiros ajudaram a estabelecer a geodésia, a ciência da forma e tamanho da Terra. E ele estava certo: a Terra não é perfeitamente redonda. Ela se projeta no equador e se achata nos polos—detalhes que são fundamentais ao projetar sistemas de satélites ou calcular coordenadas globais precisas.

Curiosidades Sobre Elipsóides

• A Terra não é uma esfera perfeita—é um elipsóide oblato, ou seja, é um pouco mais larga no equador. A diferença é de apenas alguns milímetros em escala, mas é importante para o GPS e navegação espacial.
• Ovos são elipsóides naturais próximos. Embora não perfeitos, ovos de galinha se assemelham o suficiente a elipsóides para que cientistas usem fórmulas de elipsóide para estimar seu volume em pesquisas agrícolas.
• Muitas rochas espaciais e luas têm forma elipsóide, não esférica. Isso acontece porque sua gravidade não é forte o suficiente para moldá-las em esferas perfeitas.
• A imagem médica também usa elipsóides. Técnicas de ressonância magnética (MRI) e ultrassom frequentemente estimam o volume de órgãos com aproximações elipsóides—é uma maneira eficiente de obter medições úteis sem necessidade de escaneamentos 3D completos.

Você encontrará esta e dezenas de outras calculadoras úteis na biblioteca completa de Ferramentas Matemáticas, projetada para estudantes, educadores e profissionais.