Conversor de Ângulos

Ângulos estão em toda parte. Eles definem os cantos da sua casa, a inclinação da Terra e até a forma como a cena do seu filme favorito é filmada. Embora a ferramenta conversor de ângulos torne fácil alternar entre graus, radianos e revoluções, o conceito de ângulo tem uma história rica, utilidade prática e significado universal. Desde os astrônomos babilônios que mapeavam estrelas até os engenheiros modernos projetando pontes, os ângulos nos ajudam a entender espaço e movimento. Eles são fundamentais na matemática, na física, na arte e até na filosofia. Neste artigo, não vamos apenas explicar como converter ângulos — vamos mostrar por que eles importam na ciência, na cultura e no dia a dia. Se você é estudante, pesquisador ou leitor curioso, essa jornada vai revelar como algo tão simples quanto uma curva ou um canto pode desvendar a geometria oculta do universo.

O que é um ângulo?

Um ângulo é mais do que um vértice pontudo em um diagrama — é um conceito fundamental para entender e descrever o mundo ao nosso redor. Segundo o Instituto Nacional de Padrões e Tecnologia dos EUA (NIST), um ângulo é “a figura formada por dois raios que têm um ponto inicial em comum” e é medido pela quantidade de rotação que um raio precisa fazer para se alinhar ao outro.

Na prática, ângulos estão em todo lugar — desde a forma como inclinamos a cabeça até como construímos pontes e orientamos satélites. Eles nos ajudam a interpretar direção, orientação e até equilíbrio. Sem ângulos, a geometria deixaria de existir, a engenharia seria um palpite e o movimento ficaria sem sentido matemático.

Os ângulos apresentam várias formas:

Cada tipo tem relevância prática. Ângulos agudos e retos predominam em estruturas comuns — paredes, telas e bordas de papel — enquanto obtusos e reflexos aparecem em design, arquitetura e biomecânica. Na física, o movimento angular define tudo, desde órbitas planetárias até o giro de elétrons. Mesmo na percepção, ângulos importam: nossa percepção de profundidade depende dos ângulos visuais formados pelos olhos.

Graus, Radianos e Revoluções

Ângulos podem parecer simples à primeira vista, mas sua forma de medição evoluiu ao longo da história, da matemática e até da cultura. As três unidades mais comuns — graus, radianos e revoluções — formam um sistema universal que nos permite descrever rotação, orientação e movimento em diferentes áreas.

A Relação Fundamental

A rotação completa de um círculo é representada de três maneiras equivalentes:

A partir daí, derivamos as conversões principais:

Essas equivalências não são só para matemáticos — elas sustentam desde animações digitais até cálculos de órbita em voos espaciais.

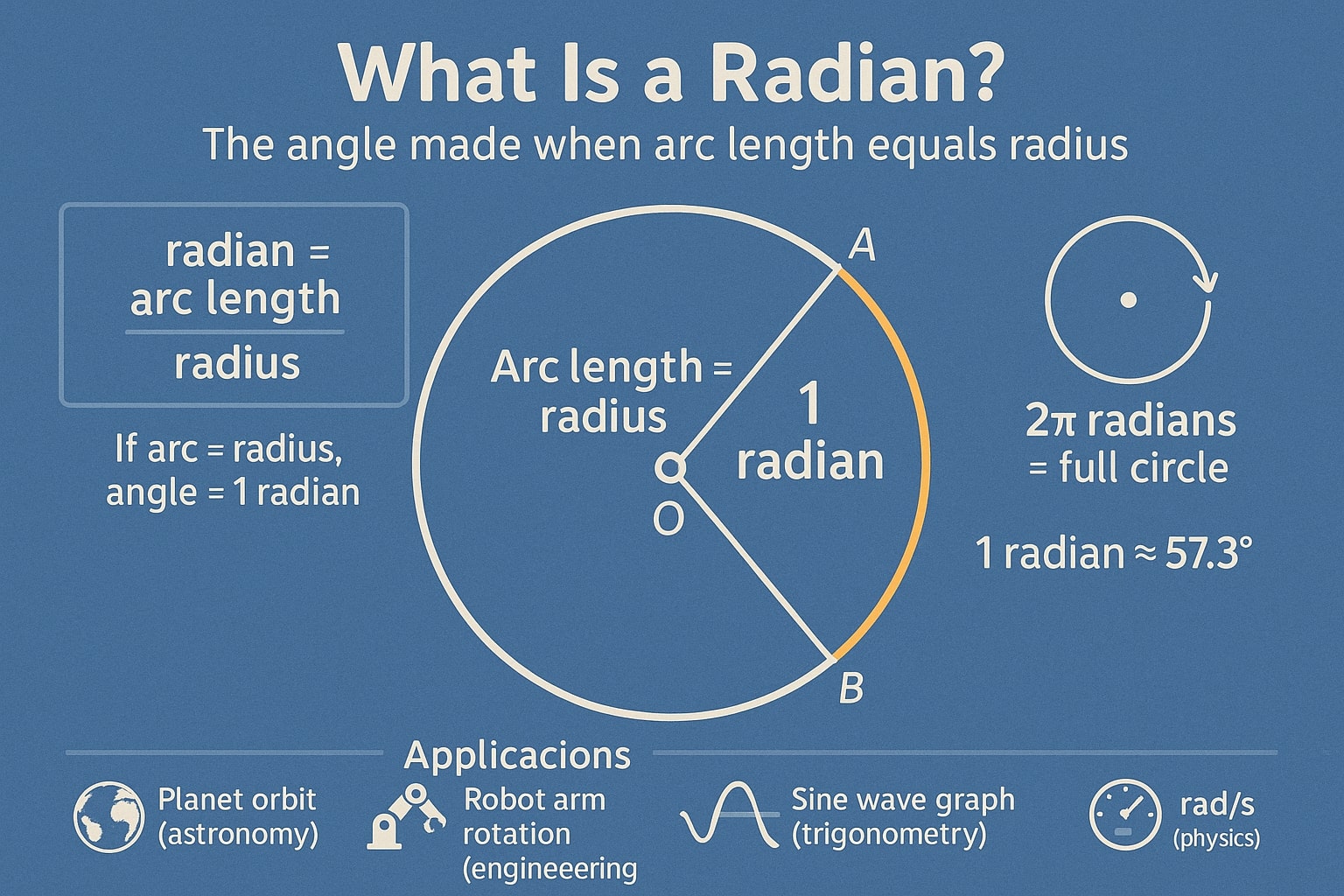
O que é um radiano?

Radianos são a unidade padrão de medida angular na matemática avançada e na física. Eles se baseiam no raio de um círculo. Um radiano é definido como o ângulo cujo arco tem o mesmo comprimento do raio do círculo.
Matematicamente:

radian = comprimento do arco / raio

Como a circunferência de um círculo é 2πr, uma rotação completa equivale a 2π radianos.
Logo:

Radianos simplificam muitas fórmulas matemáticas, especialmente em cálculo, onde funções trigonométricas se comportam de maneira mais natural.

Fórmulas Básicas de Conversão

Essas fórmulas permitem conversões perfeitas entre sistemas, seja programando, traçando gráficos ou interpretando medições científicas.

Tabela de Referência Rápida para Ângulos Comuns

Essa tabela é útil para estudantes e profissionais que trabalham com funções trigonométricas, movimento circular ou ambientes de programação como JavaScript e Python.

Erros Comuns em Conversão de Ângulos

• Esquecer de mudar o modo da calculadora: Muitos estudantes usam graus quando deveriam estar em radianos (ou vice-versa), gerando resultados errados em trigonometria.

• Arredondar π cedo demais: Isso causa perda de precisão — especialmente em aplicações de física e engenharia.

• Confundir símbolos e premissas: Alguns softwares científicos assumem que ângulos estão em radianos, a menos que se especifique o contrário. Sempre verifique a unidade esperada.

Relação Ângulo–Tempo em Sistemas Reais

Em um mundo cada vez mais baseado em precisão, do design digital à navegação aeroespacial, os ângulos são essenciais para medir, modelar e se mover no tempo. Toda rotação, trajetória ou alinhamento estrutural depende de medições angulares exatas — muitas vezes em tempo real.

Seja você um estudante calculando radianos ou um engenheiro ajustando a orientação de um satélite, o conversor de ângulos é fundamental. Ele não só economiza tempo — ele honra o tempo, garantindo transições perfeitas entre graus, radianos e revoluções, sem margem para erro.

Relógio Analógico

• 1 volta completa = 360°

• 1 hora = 60°

• 1 minuto = 6°
   → Ângulo por minuto = 360/60 = 6°

Velocidade Angular em Robótica/Física

• Unidade padrão de velocidade de rotação: radiano/segundo (rad/s)

• Se um objeto gira θ radianos em t segundos:
   →

onde ω é a velocidade angular

Revoluções e Rotação Temporal

• 1 revolução = 360° = 2π radianos

• Tempo por rotação:
   → Tempo por rev = 1/Revoluções por segundo

Euclides – O Pai dos Ângulos

Muito antes de existirem calculadoras ou conversores de ângulos, um homem moldou a maneira como entendemos o espaço: Euclides de Alexandria, frequentemente chamado de “pai da geometria”. Por volta de 300 a.C., sua obra seminal Elementos lançou as bases da geometria moderna — e com ela, nosso conceito de ângulo.

Em Elementos, Euclides não só definiu o ângulo, mas o sistematizou. Ele descreveu o ângulo reto como o resultado de uma linha reta que, ao incidir sobre outra, divide em partes iguais os ângulos adjacentes — um momento de equilíbrio e simetria que guiaria arquitetos e cientistas por milênios.

A abordagem rigorosa de Euclides ajudou a diferenciar ângulos não apenas pela medida, mas pela relação entre eles. Seus princípios continuam influenciando arquitetura, astronomia e até gráficos computacionais. Sem Euclides, um ângulo de 90° talvez nunca tivesse se tornado “reto” — não só no valor, mas também no nome.

Para explorar outras ferramentas como esta, visite a categoria Conversão — sua porta de entrada para cálculos mais inteligentes, rápidos e precisos em física, matemática e aplicações práticas.